| 제목 | 답변완료 6강 마지막 부분에 예제 2번 | ||
|---|---|---|---|
| 질문유형 | 강좌내용 | 교수님 | 김예석 |
| 과목 | 동역학 | 강좌명 | |
| 작성자 | 김*석 (k*****8) | 등록일 | 2019-01-31 17:53 |
|
예제 2번 문제 pdf 파일로 안 올라와 있는것 같습니다.
1-4 와 2-1 에 올린 pdf 봤는데 없더라구요. 답변 완료된 질문과 답변은 수정 및 삭제가 불가합니다. |
|||
- 댓글
- 0
아, 미안합니다.
찾아보니, 제가 PDF로 올리지 않았어요... ㅠㅠ
다행히도 문제는 잘 보이니.. 동영상으로 확인 부탁 드립니다.
곡률반지름은 아래처럼 공식을 유도할 수 있습니다.
(아래 글은 네이버 지식인에서 가져왔습니다.)
================================================================
곡선의 곡률이란, 곡선이 이동한 거리 s에 따른 기울기의 변화율입니다.
즉,
곡선에서 이동한 거리를 s라고 하고, 기울기의 변화를 θ라고 하면,
이때의 방향변화율 κ는
κ = lim(Δs->0) abs(dθ / ds)
(abs = 절대값)
으로 정의할 수 있겠죠
이 곡선이 x축에 거의 접하는 점에서 생각해 보면,
tanθ = dy/dx =y` 이고, θ=arctan(dy/dx)
(arctan = tan-1 . 탄젠트의 역함수)
ds² = dx² + dy² 에서
ds² = (1+ (dy/dx)² )dx²
(ds/dx)^2 = (1+ (dy/dx)²)
ds/dx = (1+ (dy/dx)^2) ^ 1/2
(참고 : arctan(y)` = 1/(1+y^2) dy )
계산해주면
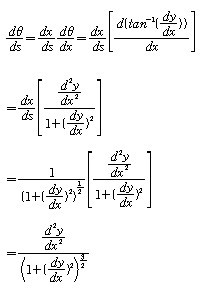
이 되고, 곡률반지름은 1/κ 이므로 이것의 역수를 취해주면 됩니다.
- 2019-01-31
- 2024-12-12 수정




























