| 제목 | 답변완료 24강 31분쯤에 Gradient Operator와 Tensor의 내적 | ||
|---|---|---|---|
| 질문유형 | 강좌내용 | 교수님 | 권준표 |
| 과목 | 유체역학 | 강좌명 | |
| 작성자 | 신*열 (b**********r) | 등록일 | 2019-05-25 18:45 |
|
학부과정에서 ∇·a(a는 벡터)에 대해서는 a에 대한 divergence라고도 하며, 성분끼리의 곱, 즉 벡터의 내적 연산처럼 하면 된다고 명확하게 설명이 되어 있습니다. 그런데 ∇· σij와 같은 연산의 경우에(σij 는 텐서), σij 는 i,j,k성분으로 어떻게 나타나서 ∇ 와의 도트곱이 나타난다던지 하는 연산의 개념도 모르고 애초에 텐서에 대해부터 학부과정에서 잘 모르잖아요. 결론적으로 말하자면 ∇· σij 연산법 자체에 대해서 먼저 설명이 좀 더 상세하게 이루어져야 할 것 같습니다. 책을 볼 때 구체적인 설명 없이 Gradient Operator와 Tensor의 도트곱이 나오는데 혼란스럽더라구요. ∇· σij 연산에 대해 설명을 좀 구체적으로 해주시면 감사하겠습니다. 강의에서는 좀 두루뭉술하게 넘어가는듯한 느낌을 받았는데 구체적으로 설명을 들어야 명쾌하게 넘어갈 수 있을 것 같습니다. 나아가 tensor의 연산에 대한 일반적인 수학적 이론에 대해서도 좀 질문을 부탁드려도 될지요? 합과 차는 성분끼리 하면 될 것 같은 직관인데, 제가 이 글에서 먼저 질문드린 형태의 곱이라던지 tensor라는 개념을 도입함으로서 처음 접하게 되는 연산에 대해서 좀 알고 싶습니다. 감사합니다.
답변 완료된 질문과 답변은 수정 및 삭제가 불가합니다. |
|||
- 댓글
- 0
안녕하세요. 벡터함수의 미분학은 사실 1-2학년에 배우는 일반수학, 공학수학과 관련된 범위이고, Tensor의 경우도 크게 다르지는 않습니다. 이를 설명하기 위해서는 최소한 1시간의 강의가 필요하기 때문에 글로써는 답변이 많이 어려울 것 같습니다. 또한 탄성학이나 연속체역학 등의 강의를 들으면 여러가지 연산에 대한 기초를 다시 배울 것이기 때문에 너무 걱정하지 않으셔도 됩니다.
저는 ∇(Grad)에 한정하여 답변드리겠습니다. Divergence, Curl 등도 같이 설명드리면 좋겠으나 나머지는 공학수학을 다시 복습해보시길 바랍니다.
벡터함수의 미분 연산자(vector differential operator, ∇)의 정의는 아래와 같습니다.
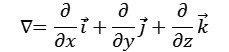
그리고 임의의 Stress를 Tensor로 표현하면 아래와 같습니다. (tau대신 모두 sigma로 표기합니다.)
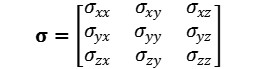
그리고 이 텐서를 미분하여, 즉 ∇σ 하고 i, j, k 방향으로 표현하면 아래와 같습니다.
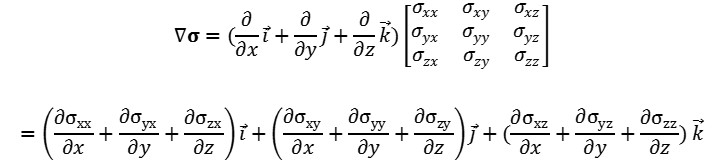
여기까지의 과정이 질문에 대한 충분한 답이 되었을 거라 생각합니다.
감사합니다.
- 2019-05-27
- 2024-12-12 수정






























