| 제목 | 답변완료 고체역학 21강(5-2강) 예제풀이 질문입니다. | ||
|---|---|---|---|
| 질문유형 | 강좌내용 | 교수님 | 권준표 |
| 과목 | 고체역학 | 강좌명 | |
| 작성자 | 송*엽 (s*******3) | 등록일 | 2024-02-14 01:06 |
| 첨부파일 | |||
|
고체역학 퍼펙트 완성 21강 6분 I를 구할 때 중립축 즉, z축에 대해서 구해야 하기 때문에 Izz를 구해야 한다고 말씀하셨는데 길쭉한 면을 기준으로 봤을 때 중립축은 x축이 되는 것이 아닌가요 I를 구할 때 어떤 이유에서 단면을 기준으로 구해야하는지 궁금합니다.
#굽힘응력 #면적관성모멘트 #중립축 답변 완료된 질문과 답변은 수정 및 삭제가 불가합니다. |
|||
- 댓글
- 0
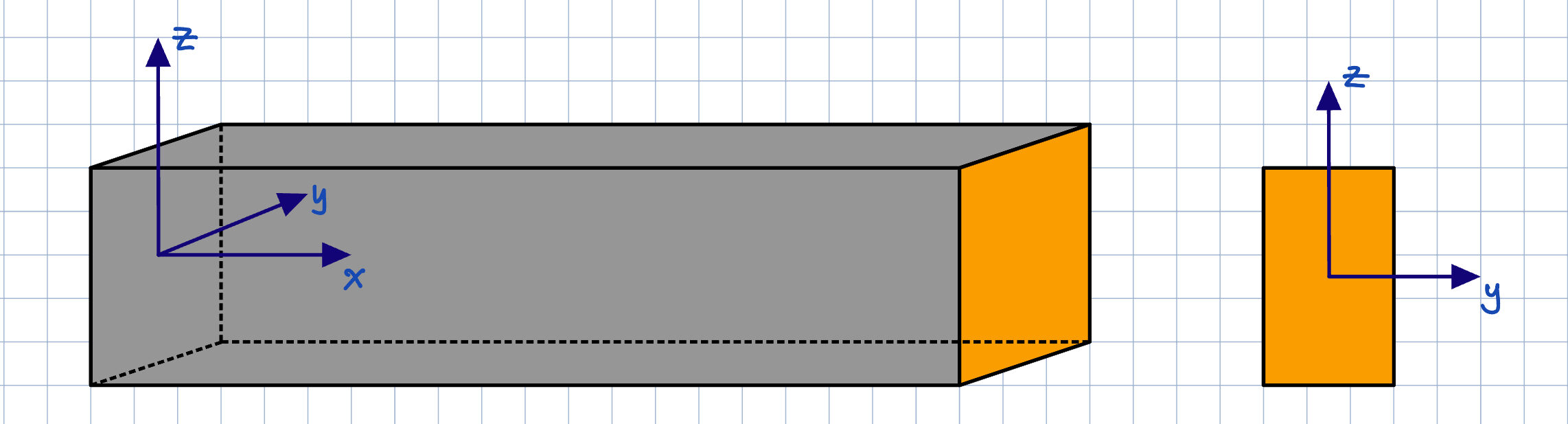
3차원이라서 축방향에 대해서 살짝 헷갈리신 것 같습니다. 아래의 그림과 2차 단면 모멘트에 대한 설명을 보시면, 충분히 이해가 되실 겁니다. 2차 단면 모멘트의 단면의 기준은 관심 있는 모멘트 또는 처짐 방향에 따라 결정됩니다.
Izz라는 용어는 ƈ차 단면 모멘트` 또는 `단면 이차 모멘트`를 나타내는 데 사용되며, 이는 구조물의 휨 강성을 결정하는 데 중요한 값입니다. `I`는 이차 모멘트를 나타내는 기호이고, `zz`는 모멘트를 적용하는 축을 나타냅니다. 일반적으로 단면 이차 모멘트는 축에 대해 적분하여 계산되며, 이 경우 z축에 대한 단면 이차 모멘트를 나타내는 것입니다.
굽힘 모멘트는 힘이 작용하는 평면과 수직인 축을 중심으로 발생하므로, 바(beam)의 경우 X축 방향으로 놓여 있을 때, 종종 해당 수직 축은 Z축으로 고려됩니다. 따라서 Izz는 Z축 주위의 바의 굽힘 강성을 결정하는 데 사용되는 수치입니다.
단면의 Izz는 다음과 같은 식으로 계산됩니다:
[ I_{zz} = ∫ y² dA ]
여기서 dA는 단면의 미소 면적 요소이고, y는 Z축으로부터의 거리입니다. 이 계산은 단면 전체에 대해 수행되어, 전체 단면의 굽힘에 대한 저항성을 평가합니다.
- 2024-03-04
- 2024-12-12 수정





























